Spiking Dynamical Systems

The human brain offers a computational paradigm distinct from both digital and quantum. It can be orders of magnitude more energy-efficient than digital architectures and is better poised to handle the noisy, ill-conditioned inputs typical of biological sensing. These advantages have motivated the development of neuromorphic computing—a field that seeks to replicate the brain’s computational principles. Despite its potential, neuromorphic computing has yet to deliver the transformative breakthroughs it envisioned. One major bottleneck is the prohibitive computational cost of simulating and analyzing spiking neurons. This makes the study and design of large-scale spiking networks, which are essential in capturing many interesting phenomena and behaviors, a resource-intensive task, as evidenced by the billion-euro Human Brain Project.

The most common method for simulating spiking dynamics is numerical integration algorithms. Nevertheless, this class of algorithms does not provide an adequate simulation and analysis framework for the design of large-scale neuromorphic systems. These algorithms are not scalable, do not exploit the event-based structure of the behavior, and lack efficient tools for variability analysis—an essential component of any robust design framework. In response to these limitations, we propose a departure from state-space representation and incremental numerical integration methods in favor of an operator-theoretic representational language and solver framework. This approach lays the foundation for a more principled, scalable, and efficient framework for simulating and analyzing neuromorphic systems.

In this new framework, the input-output behavior of neuromorphic systems is captured using an operator (e.g., a nonlinear mapping) defined on Hilbert space. Thus, given an input signal, the problem of simulating a neuromorphic system reduces to a zero-finding problem on Hilbert space. This formalism is transformed into a fixed-point iteration problem, enabling the use of modern proximal-gradient methods of convex optimization that are known for their efficiency. This operator-theoretic framework resolves the scalability issue (through using first-order methods and restricting the search space) and offers an efficient variability analysis toolbox.

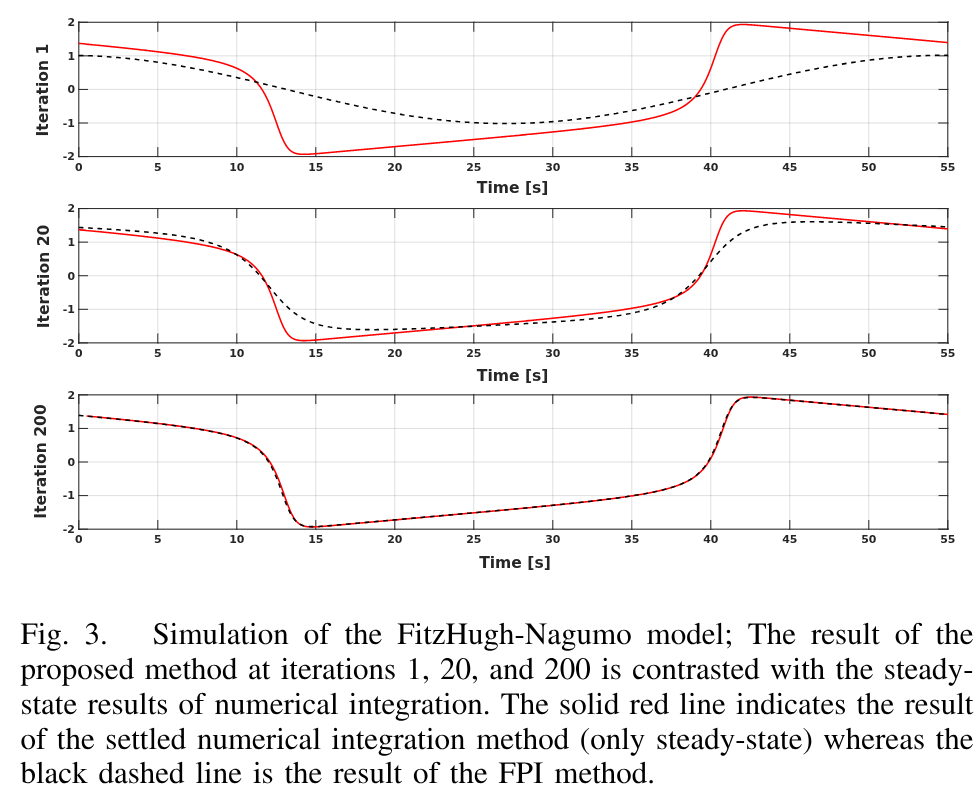
A key promise of the proposed operator-theoretic framework is its ability to modulate the scale at which neuromorphic systems are modeled, simulated, and analyzed. By adjusting this scale, it is possible to transition from coarse mean-field estimates of the network to fine-grained and accurate simulations at the neuron level. In fact, this tunable resolution not only enables more flexible analysis but also bridges the micro- and macro-scale perspectives, offering a unified and principled understanding of complex neuromorphic dynamics. This unification results in the emergence of mean-field behaviors of spiking systems that stem from the dynamics of the individual neurons, and not their high-level abstractions, an essential link that is missing from the literature.

[1] Shahhosseini, A., Chaffey, T., & Sepulchre, R. (2024, December). An operator-theoretic framework to simulate neuromorphic circuits. In 2024 IEEE 63rd Conference on Decision and Control (CDC) (pp. 6703-6708). IEEE.

[2] Shahhosseini, A., Burger, T., & Sepulchre, R. (2024, December). Variable Metric Splitting Methods for Neuromorphic Circuits Simulation. Submitted to the 2025 IEEE 64th Conference on Decision and Control (CDC). IEEE.

[3] Shahhosseini, A., Chaffey, T., & Sepulchre, R. Operator-Splitting Methods for Neuromorphic Circuit Simulation. Submitted to IEEE Transactions on Automatic Control