Poincaré Maps

This paper presents a systematic and generalizable method we developed for constructing effective Poincaré sections—an essential tool in analyzing the qualitative behavior of dynamical systems. Traditionally, selecting these sections has been more of an art than a science, relying heavily on visual intuition and limited to low-dimensional systems. We propose a geometric-statistical algorithm that automates this process, using centers of curvature and clustering to identify regions of interest in the trajectory data, then defining Poincaré sections through those regions while aligning them with the system’s local flow direction. Notably, the method is equation-agnostic, making it broadly applicable across a wide range of systems, including high-dimensional and chaotic ones purely from gathered data.

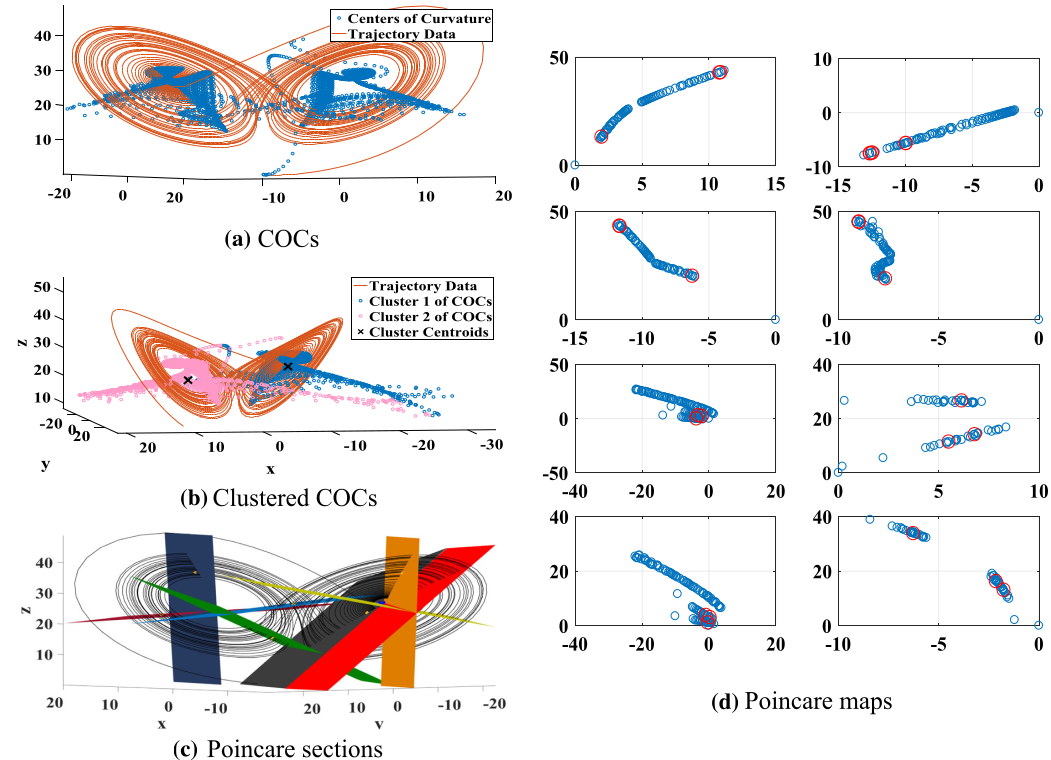
What reinforces the contribution of this paper is the use of basic tools—Euclidean geometry, clustering algorithms, and optimization—to tackle a long-standing practical challenge in nonlinear analysis. We validated the approach with several canonical examples, from the Lorenz and Rössler attractors to a 5D hyperchaotic system, showing that the method not only captures complex behaviors but does so without manual tuning, using the most basic algorithms (e.g., k-means). While the underlying mathematics is kept accessible, the approach reveals nuanced structure in the dynamics that conventional techniques might miss. It’s a framework intended to bridge methodological rigor with practical insight, and to support researchers studying systems where chaos, periodicity, or strange attractors are central. With the methodology of this paper, the first-ever higher-dimensional Poincaré maps were obtained, elevating Poincaré maps from a purely graphical tool into a statistical one.

[1]. Shahhosseini, A., Tien, M. H., & D’Souza, K. (2023). Poincare maps: a modern systematic approach toward obtaining effective sections. Nonlinear Dynamics, 111(1), 529-548.